魔術方塊有幾種組合

魔方總共有 43252003274489856000 種可能的狀態。但為什麼？

一顆三階魔術方塊在正常的打亂轉動之下，總共可以有 43252003274489856000 種不同的排列組合狀態，這個數字是這樣算的: 8! * 3^8 * 12! * 2^12 / 12

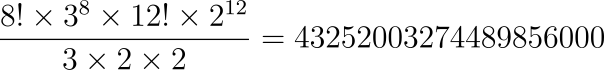
公式由來

魔術方塊是一顆一顆角塊跟邊塊組成的，所以你會看到一格一格的 – 詳情請看魔方構造這一章

一個魔術方塊的狀態長相，可以用這四個資訊來定義

魔方有 8 顆角塊 12 顆邊塊。以角塊來說，有 8*7*6*..*1 = 8! 種可能的位置排列

每顆角塊有三面，每顆都可以扭，所以就算他們在同樣位置，在那個位置每顆也有三種可能的面向，有 3 的 8 次方

邊塊也是一樣道理： 12 顆位置排列 = 12!，每顆有兩面都可以換，有 2 的 12 次方種面向可能

但是為什麼最後要除以奇怪的數字 12 (2x3x2) 呢？因為不是每個拼湊出來的組合都能夠以「正常轉動」產生！

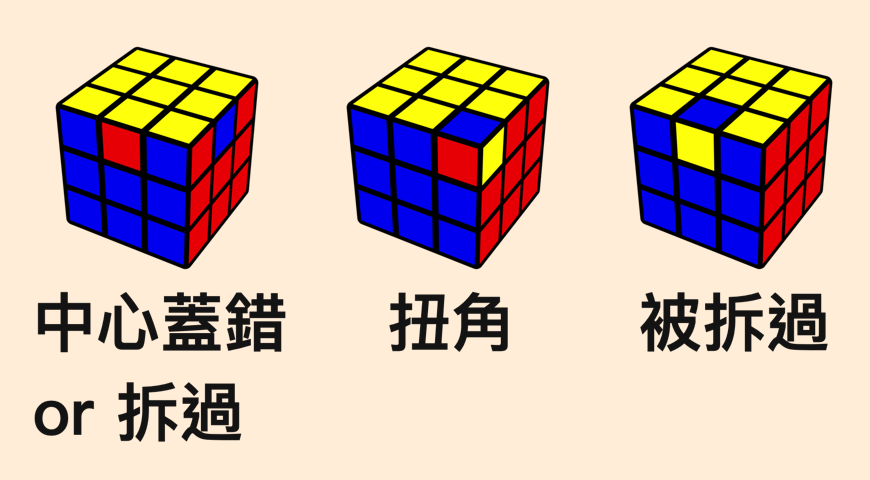
參考魔術方塊壞了解不出來這一章，有「三類」情況是不正常的魔方狀態

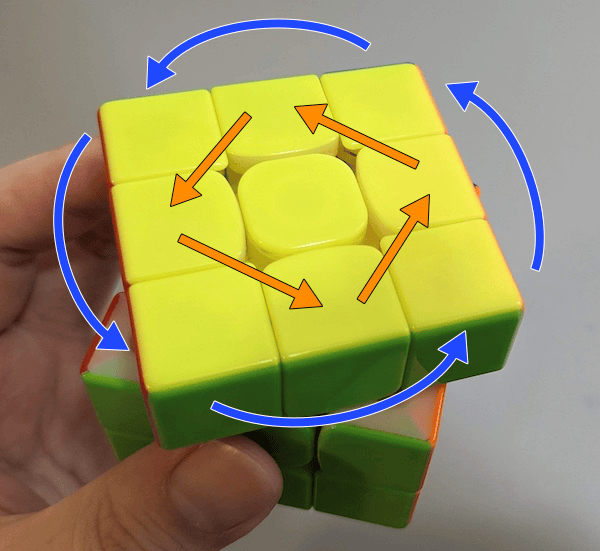
魔術方塊的一次轉動，會「輪調」四顆邊塊與四顆角塊。這種調動可以看成是三次的兩兩交換：從 1234 變到最後的 2341，可以看成

(12)34 → 2(13)4 → 23(14) → 2341

這種「兩兩交換」的奇偶性是固定的，也就是你可以有其他不同兩兩交換的方式把 1234 變成 2341，但是交換的次數都會是奇數次。所以一次正常的魔方轉動 (90度) 會讓「邊塊交換」與「角塊交換」的次數同時是奇數或同時是偶數。

以解好的魔方為例，如果角塊位置都對，但你把兩顆邊塊拔下來交換塞回去，這顆魔術方塊就沒辦法解了，因為角塊交換次數是 0，但邊塊交換次數是 1，不是同為奇數或偶數。這就是解不出來的第一個情況

這不只限於解好的方塊，只要是亂湊、亂組裝回去的魔術方塊，有一半的機會在邊角的奇偶性不一樣，也就是「位置」上會有問題

把魔術方塊固定在黃色中心向上，白色中心向下，定義角塊「面向的數值」：看每一顆角塊白色/黃色的面向，如果朝上下的話算 0，順時針扭 120 度算 1，逆時針算 2。這樣八顆角塊都有這種「面向」的數字

在正常的轉動下，這八個角塊面向加起來會是 3 的倍數

轉上層或下層，面向不會變
轉其他層，會有兩個角落 +1 (0變1, 1變2, 但2會變0)，兩個角落 -1 (2變1, 1變0, 但0會變2)。這邊的 +1 -1 因為角塊旋轉有三個面向的關係，所以更精確地講是 “mod 3” 的 +1 -1

也就是，如果隨便亂湊，八個角塊面向加起來只有三分之一的機會能被 3 整除

邊塊面向也是類似的道理：一顆邊塊不是「好」(0) 就是「壞」(1)，而一層的轉動有些會讓四顆邊塊的好壞不變，有些會讓四顆邊塊的好變壞壞變好，所以面向數字加起來能被 2 整除，也就是亂湊只有二分之一的機率會正確

反過來，有沒有其他的限制我們不知道呢？會不會不只除以 12？

由於我們有

只要魔術方塊邊角的位置跟面向符合上面的限制，就可以用這些公式慢慢地把魔方解出來 (U-perm 跟 A-perm 能各做 2 次邊塊或角壞的兩兩交換，而 T-perm 能同時改變邊角的奇偶性。然後再改變面向即可)